需要的前置技能
- 线段树(权值线段树)
- 离散化
常见应用
- 区间/树上路径第 K 大
- 区间不同数的个数
简介
主席树在算法竞赛领域由黄嘉泰(HJT)提出,故得名主席树(误?)。
主席树的结构
由若干棵线段树组成(若是权值线段树通常需先对数据离散化),按照输入顺序,每插入一个数保存一份当前版本的线段树。也就是说,对于 n 个数的输入数据,它会保存 n 棵线段树。
下面我们以求区间第 K 大的实例来讲解一下如何建立主席树。
主席树的建树过程
以输入数据 [1, 5, 8, 4, 6] 为例。我们首先将其按值离散化,即将整个数组的数值范围缩小到 [1, n],得到新的数组 [1, 3, 5, 2, 4]。
按照新数组建立权值线段树,初始为空,如图所示:
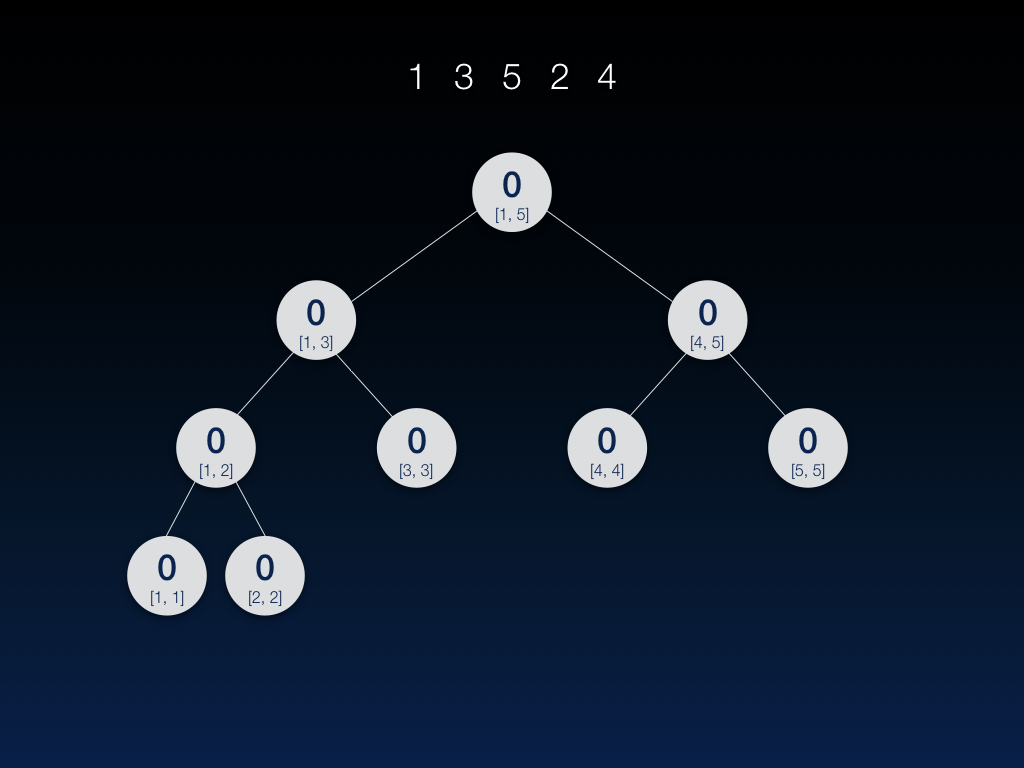
接下来我们需要按照输入顺序依次插入数据,这里我们假定 ACMers 一般都比较悠闲,把这 5 个数分成 5 天来插入。
第一天,我们插入数字 1(每天插入的数字均以不同的颜色表示),并将当天的线段树保存了一份快照:
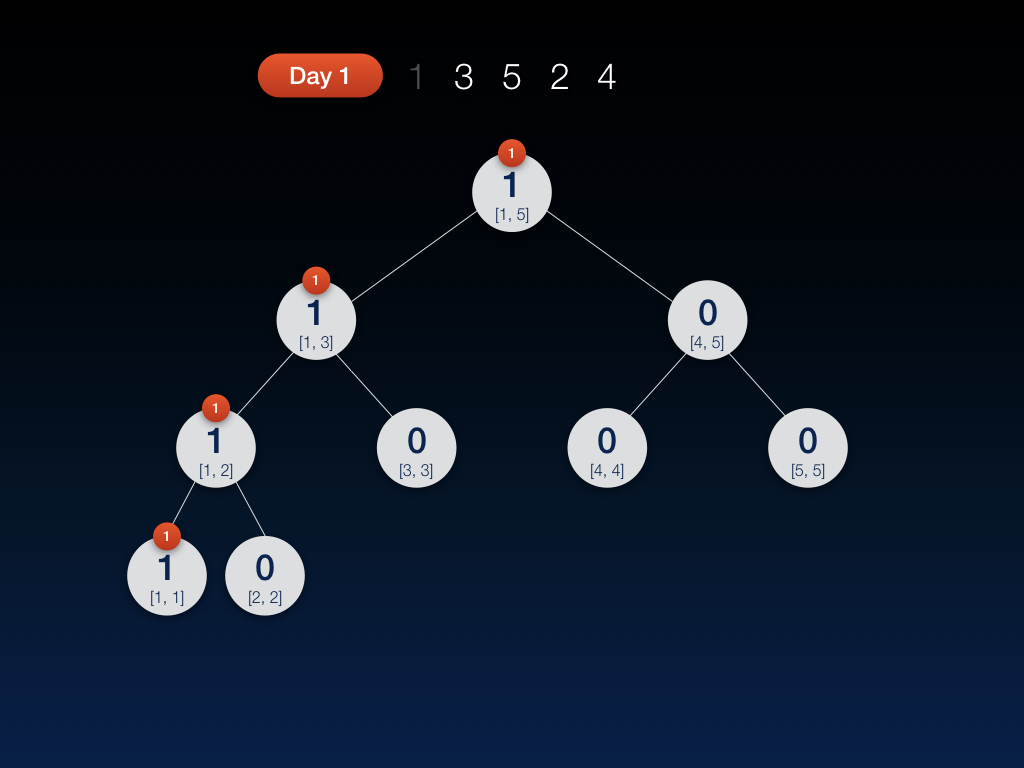
第二天,插入数字 3,并将当天的线段树保存了一份快照:
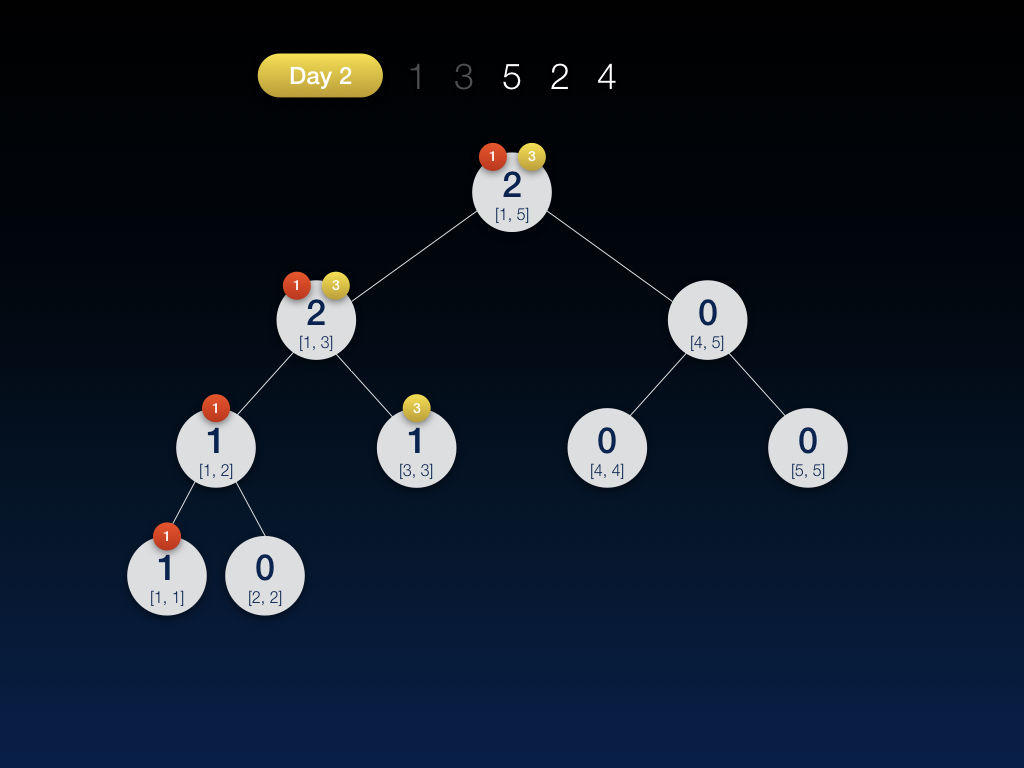
第三天,插入数字 5,并将当天的线段树保存了一份快照:
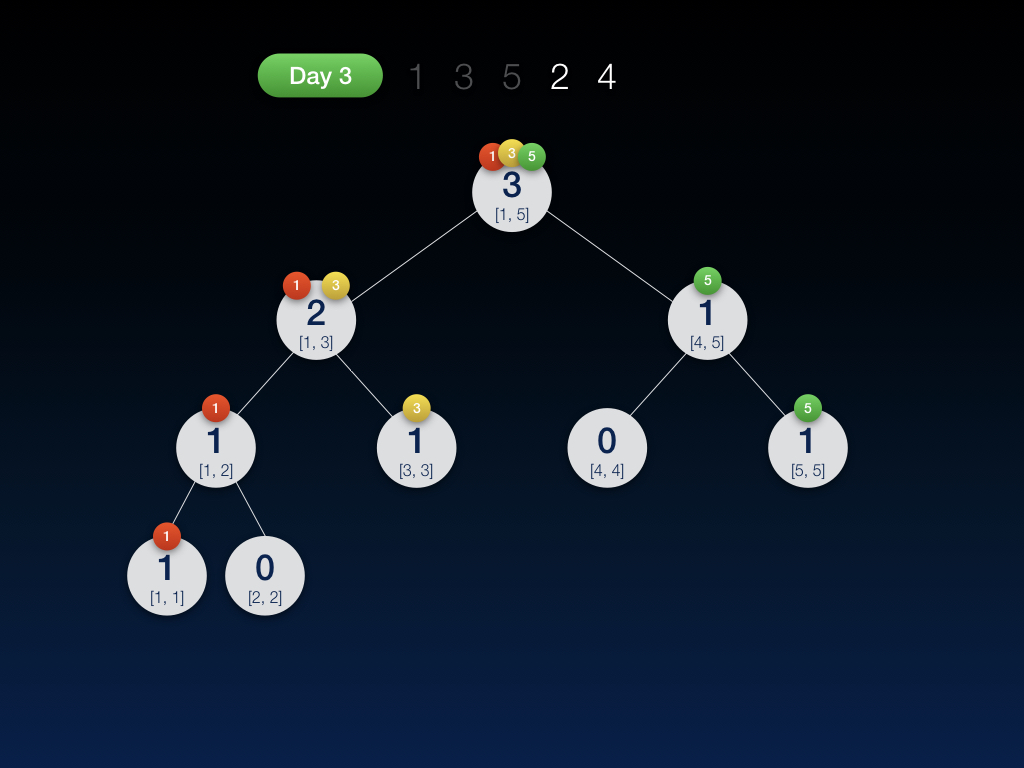
第四天,插入数字 2,并将当天的线段树保存了一份快照:
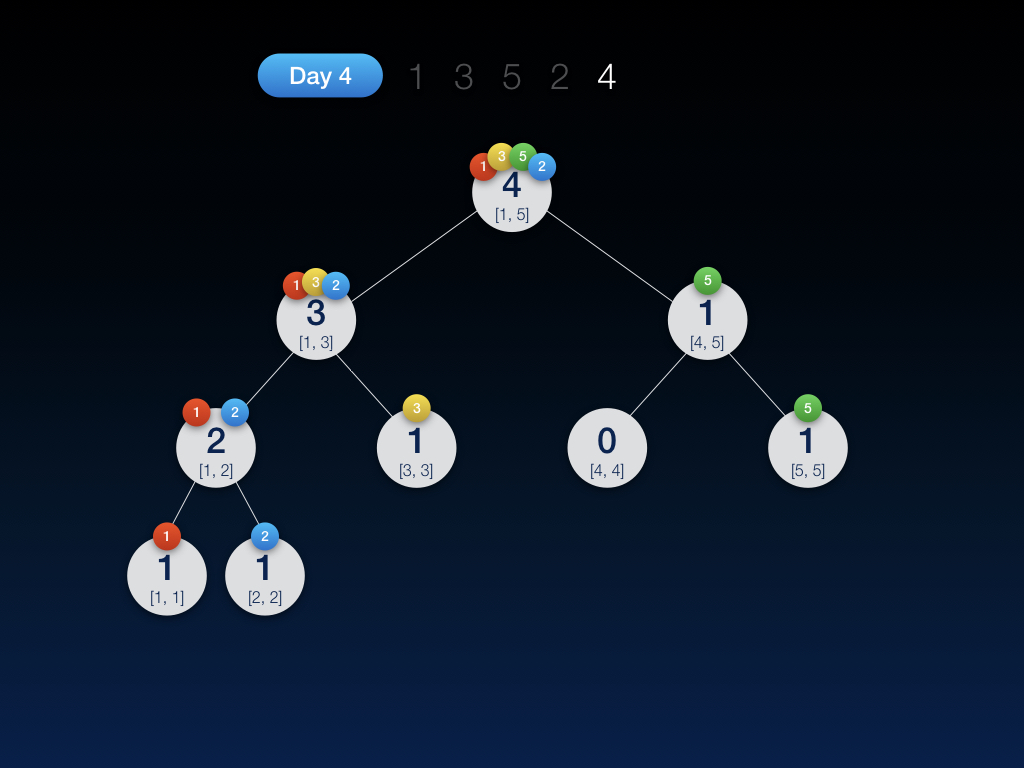
第五天,插入数字 4,并将当天的线段树保存了一份快照:
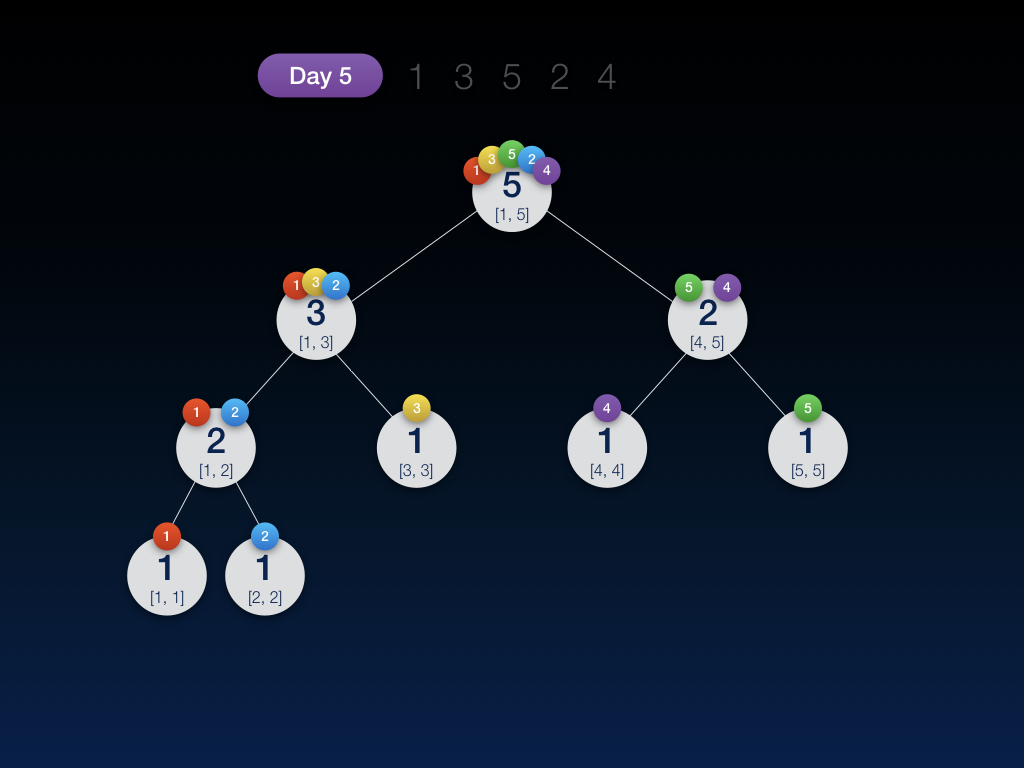
OK!插入完毕,接下来我们来瞅一下,现在手里有这 5 天的总计 5 张线段树快照:
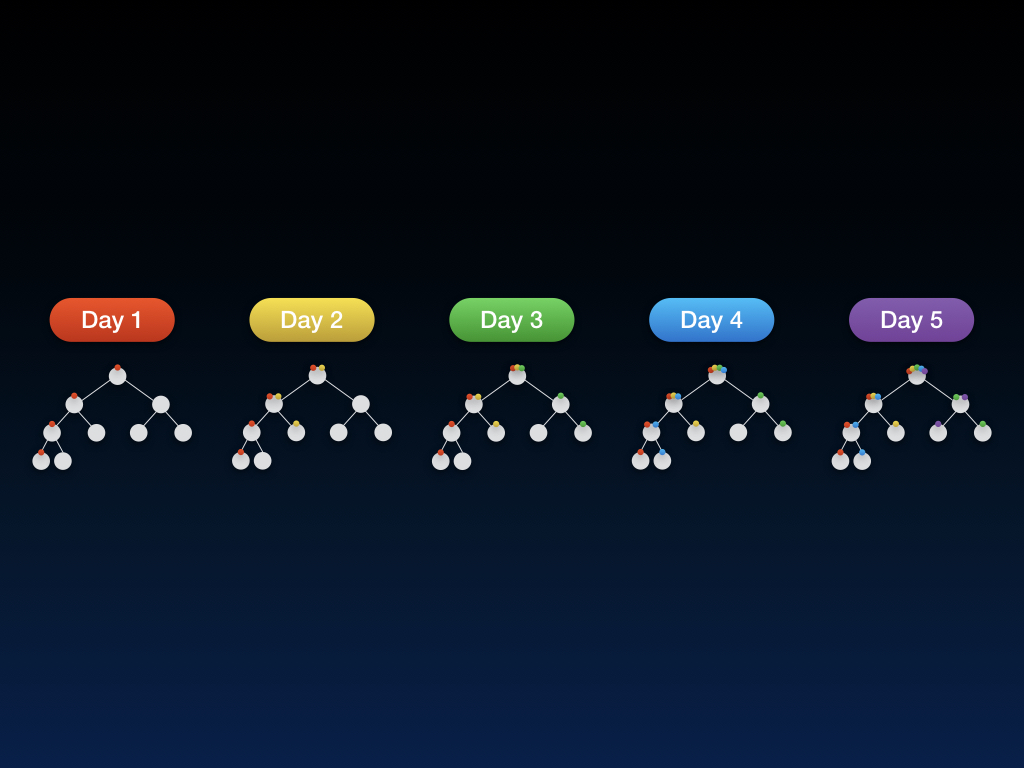
至此,主席树建树完成,时间复杂度 $O(nlogn)$。
主席树的重要性质:线段树做差
现在大家可能会问:我保存那么多线段树快照干嘛?能吃吗?我可以很负责任地告诉大家:不能。
那么我们能拿他们干什么呢?其实是很简单:线段树做差!也就是将两棵线段树两两之间对应结点数值相减,得到一棵新的线段树。
我们来试一下,将第五天和第二天的线段树做差。
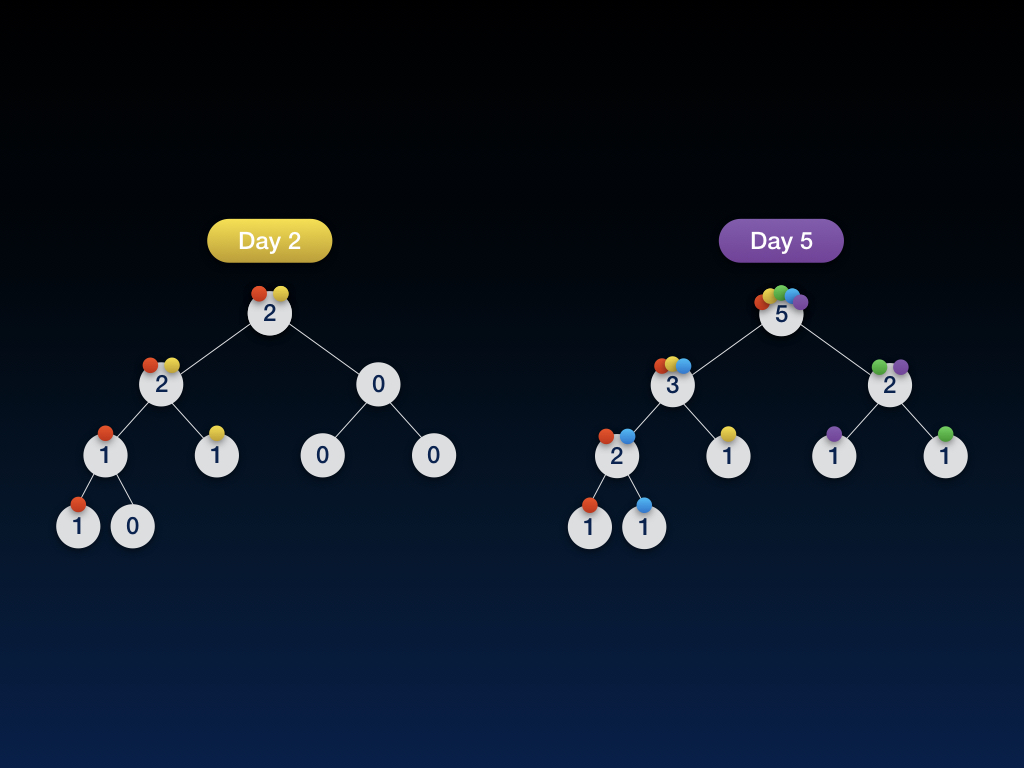
首先把他们俩的根结点取出来相减。

注意,实际运算时仅是结点上的数值相减,不包括上面的彩色的那些(除非你愿意闲得没事去建数组存这些东西),彩色的只是辅助标示这个结点上实际插入的数有哪些。
然后依次把所有结点都对应做差,得到一棵新的线段树。
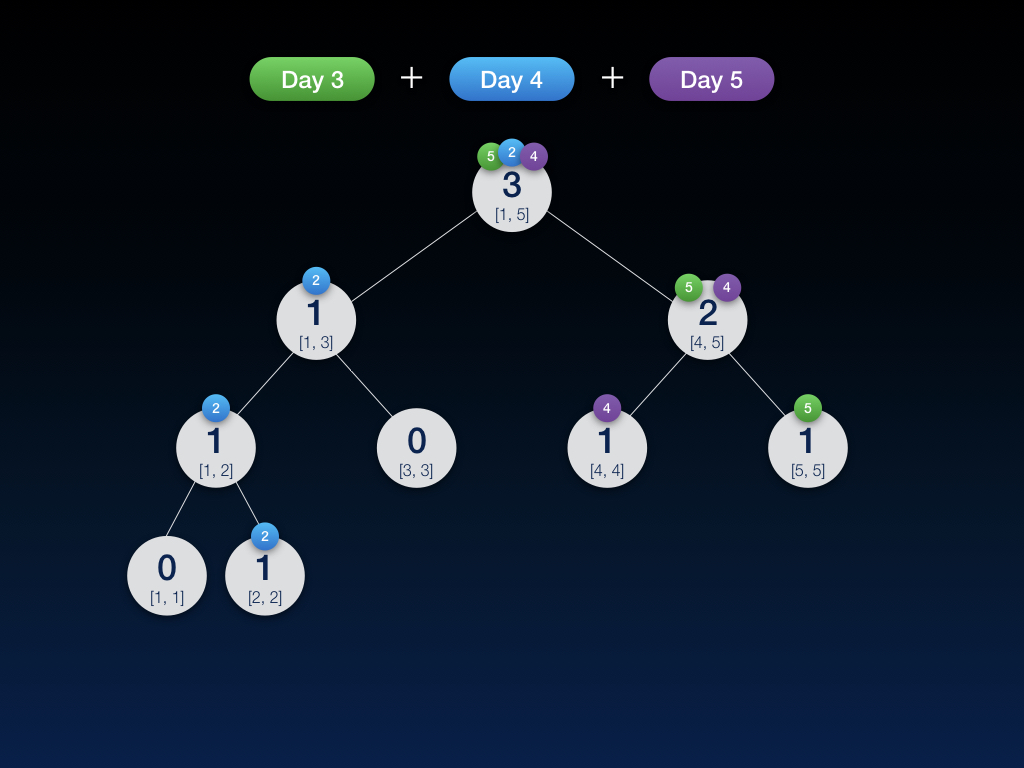
眼尖的同学应该已经发现了,做差之后的线段树是只包含第三天到第五天的线段树!是的,这就是主席树的重要性质,通过线段树做差来获取任意时间段内的线段树(也即可以获得任意范围的输入数据构成的线段树)。
主席树实战:求解区间第 K 大
主席树的基本结构和性质我们讲完了,那么现在就可以开始求区间第 K 大了(啥?这么快?)。
另外,虽说大家都习惯上说第 K 大,但是实际算法上更常用的是求第 K 小,因此下面我们都按照求第 K 小讲解。
下面直接描述一下算法过程:
- 若 K 小于等于左子树上的数值 sum,则递归到左子树找第 K 小
- 否则递归到右子树找第 K-sum 小
怎么样,是不是够简单?我们再以实例来看看,求刚才得到的第三天到第五天的线段树上(即 [3, 5] 区间)的第 2 小。
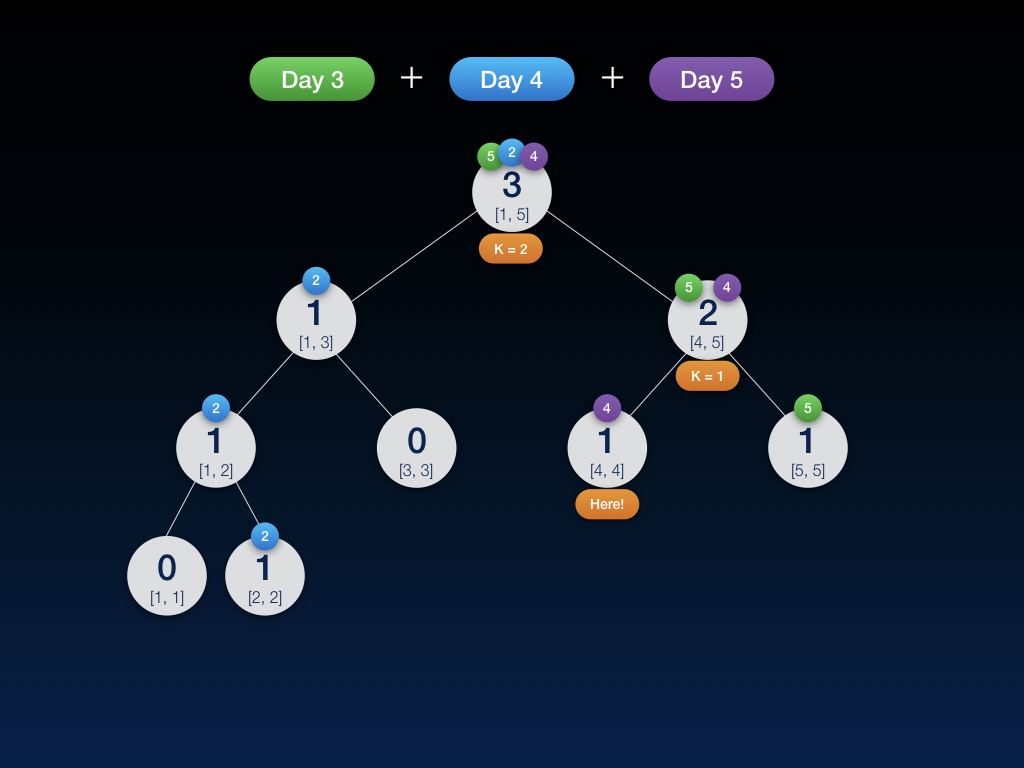
至此,我们就可以在单次 $O(logn)$ 的时间复杂度内完成查找区间第 K 大。下面我们来找一道例题提交一下试试,应该能很轻松的 1A 的。
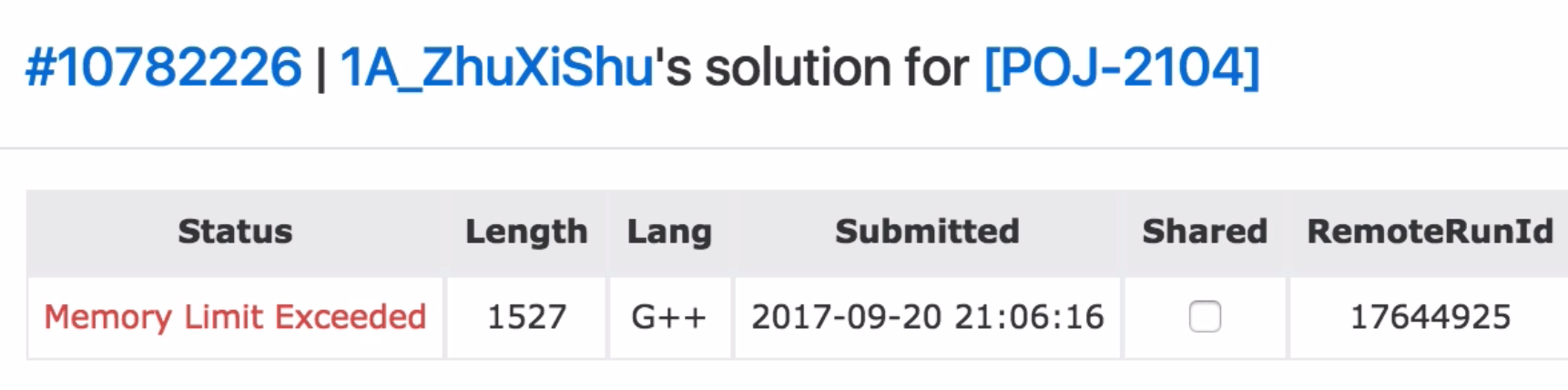
WTF?
主席树的内存优化
呃,大家也看到不小心翻车了。没错,其实你们看的是假算法。现在离开还来得及。
那么我们来分析一下原因,给大家一些选项:
- A:控制不当
- B:玄学
- C:RP 问题
- D:无可奉告
我知道大家肯定都没选对,下面来揭晓答案:
- E:爆了内存 ✔️
仔细回想一下,我们的主席树在建树过程中保留了 n 张线段树快照,也就是说空间复杂度会到 $O(n^{2})$。让我们来算一下,假设我们每个结点都是一个 int 大小,n 是 $10^{5}$,那么我们的总内存至少是上百 GiB。怎么样,是不是非常爆炸?
为了解决这个庞大的内存消耗,我们需要想一些办法。再次仔细回想一下,我们从第一天之后的每一棵线段树其实都是在上一天的基础上插入一个数形成的,而插入一个数的递归更新路径是一条树链,受影响的结点个数有 $logn$ 个,我们只需要新建这些有变化的结点就可以。因此我们就需要使用一种叫做「动态开点」的高端技术,仅在插入时新建若干个必要的线段树结点,这些结点的除了子结点指向和数值以外的属性均沿用之前结点的属性。这样就可以起到节省内存的作用。
Code
废话不多说,贴一下主席树的代码,帮助大家了解具体的实现过程。这里以 POJ 2104 为例。
|
|
总结
- 基础结构:线段树
- 可持久化:每次插入保存一个新版本,利用共用数据减少时空消耗
- 动态开点,节省内存
- 时空复杂度 $O(nlogn)$
推荐练习题
- POJ 2104:区间第 K 大
- SPOJ DQUERY:区间不同数的个数
- SPOJ COT:树上路径第 K 大
- ZOJ 2112:区间第 K 大(带单点修改)
最后
貌似还有「区间不同数的个数」和「树上路径第 K 大」没讲?大家既然都会了主席树,自行扩展一下应该是很容易的(当然似乎也可以在本博客的某些地方找到)。
另外,本文部分内容是整理自我在 2017 年 9 月给学校集训队的学弟学妹们开的算法讲堂中的幻灯片。现提供 PDF 和 幻灯片录像,大家可以自行参考(幻灯片和本文有不一致的请以本文为准,当时难免有纰漏)。
原文链接:bLue’s Blog